Ắt hẳn khi đối mặt với 1 bài toán chúng ta sẽ có nhiều giải thuật khác nhau cho nó. Việc đánh giá 1 giải thuật là tốt hay xấu khiến cho khái niệm big O ra đời. Bài viết này sẽ trình bày khái niệm big O là gì, 1 số độ phức tạp thường gặp, cách tính big O trong 1 số trường hợp.
1. Big O - Độ phức tạp của thuật toán là gì?
Lấy 1 ví dụ nhé, giữa truyền dữ liệu qua Internet và bằng chim bồ câu bạn nghĩ việc nào sẽ nhanh hơn. Chắc là khi nói tới đây, 1 số bạn sẽ cho rằng chim bồ câu - 1 phương pháp đã ra đời cách đây hơn 3000 năm lại đem so sánh với Internet - 1 phương pháp hiện đại mới xuất hiện trong khoảng 100 năm trở lại đây liệu có phải là quá khập khiễng? Câu chuyện xảy ra vào năm 2009, 1 công ty ở Nam Phi đã làm 1 thử nghiệm nhỏ. Họ có 2 chi nhánh ở cách nhau 50 dặm, 1 đường truyền Internet (ở mức khá chậm). Thử nghiệm được tiến hành với 1 lương dữ liệu lớn. Mục đích của họ là truyền dữ liệu ở chi nhánh này sang chi nhánh kia. Tiến hành thử nghiệm, họ buộc những chiếc USB lại thành từng bó, buộc vào chân chim bồ câu và cho chim bồ câu bay từ chi nhánh này sang chi nhánh kia. Cùng lúc đó, dữ liệu cũng được truyền qua Internet. Và phần thắng cuối cùng đã thuộc về chú chim bồ câu. Vậy nguyên nhân là do đâu?
Hãy nhớ lại mình đã nói gì? "Thử nghiệm được thực hiện với lượng dữ liệu LỚN." Nguyên nhân cốt lõi của vấn đề nằm ở đây. Với lượng dữ liệu càng lớn, thời gian truyền tải dữ liệu qua Internet cũng sẽ càng tăng lên (với cùng 1 đường truyền mạng khi bạn download 1 file với dung lượng 1GB sẽ nhanh hơn file với dung lượng 10GB), trong khi với chim bồ câu, khi lượng dữ liệu tăng lên việc của nó là bay 50 dặm (với lượng USB được buộc vào chân tăng lên và trong sức chịu đựng của bồ câu) mặc cho lượng dữ liệu có tăng lên thì quãng đường đó vẫn là 50 dặm. Qua ví dụ trên có thể thấy khi lượng dữ liệu tăng lên thì thời gian truyền tải qua Internet sẽ tăng lên trong khi thời gian truyền tải bằng chim bồ câu vẫn không đổi. Trong trường hợp này ta nói việc truyền tải dữ liệu bằng chim bồ câu có có độ phức tạp hằng số còn qua Internet có độ phức tạp phụ thuộc vào lượng dữ liệu cần truyền tải.
Khái niệm độ phức tạp là gì có thể hiểu đơn giản là độ tương quan giữa thời gian chạy của thuật toán với độ lớn của dữ liệu đầu vào.
2. Một số độ phức tạp thường gặp:
O(n): Độ phức tạp tuyến tính. Xét hàm tính tổng các số từ 1 đến n sau:
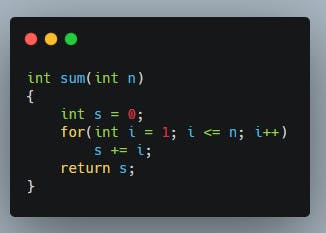
Với mỗi giá trị khác nhau của n thì số lần thực thi của vòng lặp trên là n lần. Chính vì vậy thời gian thực thi của chương trình trên phụ thuộc vào giá trị đầu vào n. Ta nói độ phức tạp của chương trình trên là O(n) (thực ra là O(n+2)).
O(1): Độ phức tạp hằng số. Cũng là bài toán tính tổng các số từ 1 đến n. Xét đoạn chương trình sau:
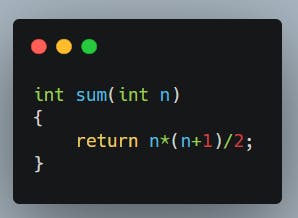
Không giống như hàm tính tổng ở trên, với đoạn chương trình này với mọi giá trị đầu vào chương trình chỉ thực thi đúng 1 câu lệnh return. Do đó, ta nói độ phức tạp của chương trình trên là O(1).
O(n²): Thường gặp khi có 2 vòng lặp lồng nhau. Xét hàm sắp xếp đổi chỗ trực tiếp (interchange Sort) sau:
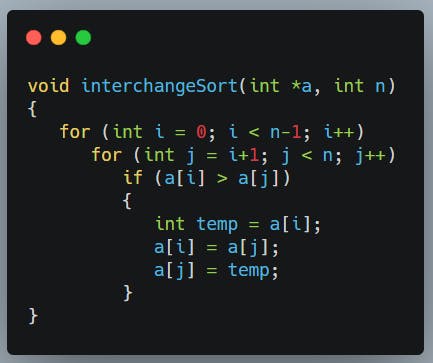
Trong hàm này, i sẽ chạy từ 0 đến n - 2. Ứng với mỗi giá trị của i vòng for trong sẽ chạy n - i - 1 lần (j từ i + 1 đến n - 1), do đó số phép so sánh cần thực hiện sẽ là Σ(n - i - 1) (với i chạy từ 0 đến n - 2) = (n - 1) + (n - 2) + (n - 3) +...+ 2 + 1 = (n - 1)*n/2 = n²/2 - n/2. Ta nói độ phức tạp của thuật toán trên là O(n²) (thực ra là O(n²/2 - n/2)).
O(logn):
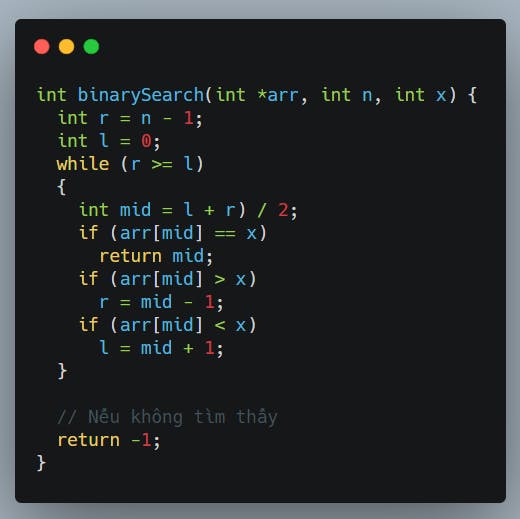
Hiểu đơn giản thì thuật toán này để tìm kiếm 1 phần tử có giá trị x có trong mảng arr đã được sắp xếp tăng dần. Để tìm được giá trị đó, ý tưởng là chúng ta sẽ lần lượt phân hoạch mảng ra làm đôi, xét phần tử ở giữa, nếu phần tử đó lớn hơn giá trị cần tìm thì xét tiếp nửa bên trái của phần tử đó, ngược lại thì xét nửa bên phải, và tiếp tục phân hoạch như thế cho đến khi tìm ra phần tử có giá trị cần tìm (có thể không tìm thấy nếu giá trị cần tìm không có trong mảng). Trong trường hợp xấu nhất, chúng ta sẽ phải phân hoạch cho đến khi mảng phân hoạch chỉ còn 1 phần tử (nếu đó không phải là giá trị cần tìm thì trả về - 1). Khi đó để đưa 1 mảng có n phần tử về 1 phần tử ta cần thực hiện logn (hiểu là log cơ số 2) lần phân hoạch. Do đó ta nói thuật toán trên có độ phức tạp O(logn).
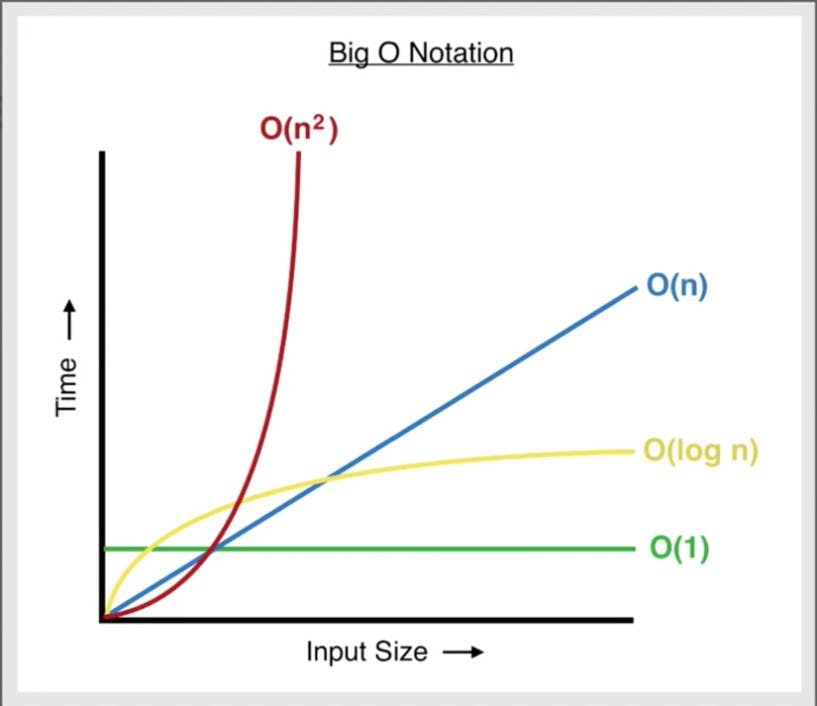
Ngoài ra còn có 1 số độ phức tạp thường gặp như O(nlogn), O(n!), O(2^n), O(n³),... Dưới đây là biểu đồ thể hiện độ hiệu quả của các độ phức tạp thường gặp.
3. Một số lưu ý để tính độ phức tạp thuật toán:
Khi xét big O, ta luôn xét với n là 1 số vô cùng lớn, do đó có thế coi n là +∞.(1) Các bước thực thi không phụ thuộc vào giá trị đầu vào(ví dụ các phép tính toán, gán, so sánh,...) có độ phức tạp hằng số(O(1)).(2) Tổng các hằng số là 1 hằng số.(3) Tích của 1 số dương với +∞ cũng là +∞, tổng của 1 số với +∞ cũng là+∞.(4) Các bước để tính độ phức tạp thuật toán:
Gọi T là độ phức tạp thuật toán cần tìm. Tính biểu thức T bằng cách cộng thời gian thực thi của các câu lệnh trong thuật toán. Xét số hạng có tốc độ tăng nhanh nhất khi n tiến đến +∞. Lược bỏ các giá trị có thể lược bỏ được theo các quy tắc ở trên. Giá trị của số hạng cuối cùng còn sót lại chính là độ phức tạp thuật toán cần tìm. Hơi khó hiểu phải không, quay lại ví dụ hàm tính tổng các số từ 1 đến n nhé:
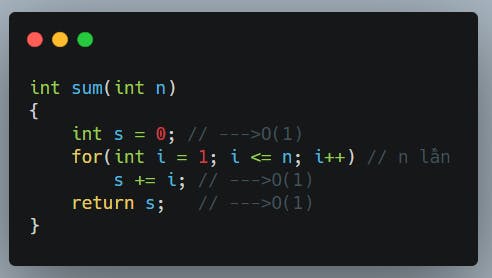
Dựa trên những gì mình đã chú thích ở trên thì trong trường hợp này T = O(1) + n x O(1) + O(1) = n x c + d (áp dụng (3), coi O(1) + O(1) là d, với c, d là các hằng số) = n (như đã nói ở trên n có thể coi là +∞, áp dụng (4) để lược bỏ c, d). = O(n).
Xét tiếp ví dụ hàm interchangeSort nhé:
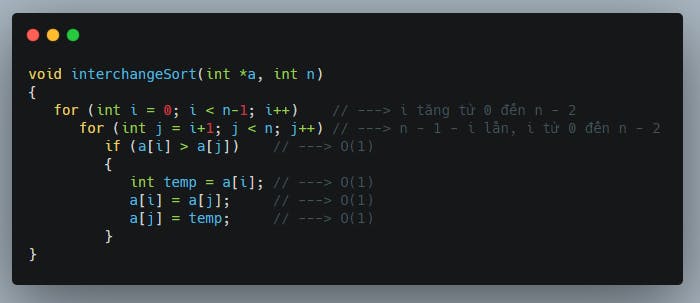
Ở phần so sánh ta thấy tất cả đều có phức tạp O(1) (không phụ thuộc giá trị đầu vào), do đó để gọn mình có thể coi cả khối lệnh so sánh là O(1) trong mỗi lần thực thi mặc cho điều kiện so sánh có xảy ra hay không. Tiếp đến để tính số lần thực thi của vòng for ta nhận thấy vòng for ở trong sẽ chạy n - 1 - i lần, với i từ 0 đến n - 2 do đó số lần chạy sẽ là ∑ (n - 1 - i) (với i từ 0 đến n - 2) = (n - 1) + (n - 2) + (n - 3) +...+ 2 + 1 = (n - 1) x n/2 = n²/2 - n/2. Do đó T = (n²/2 - n/2) x O(1) = (n²/2 - n/2) x c (với c là hằng số) = n²/2 x c - n/2 x c = n²/2 x c (do tốc độ tăng của n²/2 x c khi n tiến đến +∞ là nhanh nhất trong biểu thức trên) = n² (áp dụng (4)) = O(n²).
Tương tự các bạn có thể tính độ phức tạp của các thuật toán khác dựa trên các bước tiến hành như trên.
References:

